1.
Gambarlah grafik untuk persamaan 2x + y = 4.
Penyelesaian:
· Untuk menggambarkan grafik SPLDV, gunakan paling sedikit dua titik seperti pada tabel berikut.
· Selanjutnya, tentukan nilai untuk x = 0 dan y = 0
Untuk x = 0
2x + y = 4
2(0) + y = 4
y = 4
Untuk y = 0
2x + y = 4
2x + 0 = 4
2x = 4
x = 2
Selanjutnya, tuliskan hasil yang diperoleh ke dalam tabel.
· Sehingga, nilai atau titik yang diperoleh adalah A(0, 4) dan B(2, 0).
Kemudian, gambarkan titik tersebut ke dalam diagram Cartesius lalu hubungkan dengan sebuah garis lurus, maka akan terbentuk gambar di bawah ini.
2. Selesaikan persamaan linear dua
variabel berikut menggunakan Metode Grafik!
x + y = -2
x - y = 4
Penyelesaian:
x + y =
-2 ...(1)
x - y = 4 ...(2)
Cari titik potong grafik pada sumbu x dan y dari persamaan 1 dan 2.
· Persamaan 1
jika x = 0 maka grafik memotong sumbu y pada titik:
x + y = -2 ...(1)
(0)
+ y = -2
y = -2 (0, -2)
jika y = 0 maka grafik memotong sumbu x pada titik:
x + y = -2
...(1)
x + (0) = -2
x = -2 (-2, 0)
v Persamaan 1 melalui titik (0,
-2) dan titik (-2, 0).
· Persamaan 2
jika x = 0 maka grafik memotong sumbu y pada titik:
x - y = 4
...(2)
(0)
– y = 4
y = -4 (0, -4)
jika y = 0 maka grafik memotong
sumbu x pada titik:
x - y = 4
...(2)
x – 0 = 4
x = 4 (4, 0)
v Persamaan 2 melalui titik (0,
-4) dan titik (4, 0).
Cari titik potong kedua grafik pada bidang kordinat kartesius
untuk mengetahui penyelesaian dari persamaan linear dua variabel tersebut.
3. Tentukan himpunan penyelesaian SPLDV x + y = 5 dan x − y = 1 untuk x, y ∈ R menggunakan metode grafik.
Penyelesaian:
Pertama, kita tentukan titik potong masing-masing persamaan pada sumbu-X dan sumbu-Y
- x + y = 5
Jika titik potong dengan sumbu-X, maka y = 0
x + 0 = 5
x = 5
Titik potong (5, 0)
Titik potong dengan sumbu-Y, maka x = 0
0 + y = 5
y = 5
Titik potong (0, 5)
- x − y = 1
Titik potong dengan sumbu-X, maka y = 0
⇔ x − 0 = 1
⇔ x = 1
Titik potong (1, 0)
Titik potong dengan sumbu-Y, maka x = 0
0 − y = 1
y = −1
Titik potong (0, -1)
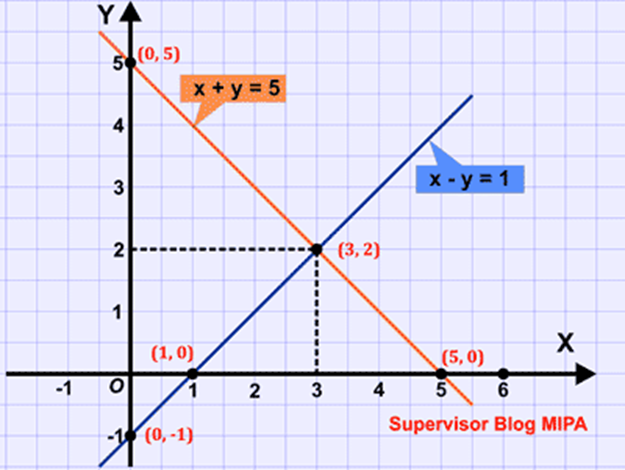
Kedua, kita gambarkan grafik dari masing-masing persamaan pada sebuah bidang Cartesius seperti yang ditunjukkan pada gambar di bawah ini.
Dari gambar grafik di atas, terlihat bahwa titik potong kedua grafik tersebut berada di titik (3, 2). Dengan demikian, himpunan penyelesaian dari sistem persamaan x + y = 5 dan x – y = 1 untuk x, y ∈ R adalah {3, 2}.
4. Tentukan himpunan penyelesaian dari sistem persamaan x + 2y = 2 dan 2x + 4y = 8 untuk x, y ∈ R menggunakan metode grafik.
Penyelesaian:
Pertama, kita tentukan titik potong masing-masing persamaan pada sumbu-X dan sumbu-Y
- x + 2y = 2
Titik potong dengan sumbu-X, syaratnya adalah y = 0
x + 2(0) = 2
x = 2
Titik potong (2, 0)
Titik potong dengan sumbu-Y, syaratnya adalah x = 0
0 + 2y = 2
2y = 2
y = 1
Titik potong (0, 1)
- 2x + 4y = 8
Titik potong dengan sumbu-X, syaratnya adalah y = 0
2x + 4(0) = 8
2x = 8
x = 4
Titik potong (4, 0)
Titik potong dengan sumbu-Y, syaratnya adalah x = 0
2(0) + 4y = 8
4y = 8
y = 2
Titik potong (0, 2)
Kedua, kita gambarkan grafik dari masing-masing persamaan pada sebuah bidang Cartesius seperti yang ditunjukkan pada gambar di bawah ini.
Berdasarkan gambar grafik sistem persamaan di atas, tampak bahwa kedua garis tersebut tidak akan pernah berpotongan karena keduanya sejajar. Dengan demikian, himpunan penyelesaian dari sistem persamaan x + 2y = 2 dan 2x + 4y = 8 adalah himpunan kosong, ditulis {} atau {∅}.
5. Sistem pertidaksamaan linear untuk daerah yang diarsir pada gambar di bawah adalah
Penyelesaian :
· Persamaan garis yang memotong sumbu X di x = 4 dan sumbu Y di y = 3 adalah 3x + 4y = 12. Tanda ketidaksamaan yang sesuai dengan daerah arsiran adalah ≥ karena arsirannya di atas garis, sehingga diperoleh pertidaksamaan linear 3x + 4y ≥ 12
· Persamaan garis yang memotong sumbu X di x = 2 dan sumbu Y di y = 6 adalah 6x + 2y = 12 atau dapat disederhanakan menjadi 3x + y = 6. Tanda ketidaksamaan yang sesuai dengan daerah arsiran adalah ≤ karena arsirannya di bawah garis, sehingga diperoleh pertidaksamaan linearnya adalah 3x + y ≤ 6
· Karena daerah arsiran terletak di kuadran pertama, maka kendala nonnegatif ( x,y tak boleh bernilai negatif).
· Sehingga diperolehlah sistem pertidaksamaan linearnya adalah
3x + 4y ≥ 12
3x + y ≤ 6
x ≥ 0
y ≥ 0






Tidak ada komentar:
Posting Komentar